離散系シミュレーション? その2
※こちらの記事は第2回です。初回をご覧になっていない方はこちらの記事からご覧ください。
みなさんこんにちは。マーケティング担当の田辺と申します。
この記事では”離散系シミュレーション”という言葉の意味・効果をご説明します。
キリの良いところがなくて前回の2倍近い超ボリュームになりましたが、もしよろしければ最後までご覧下さい。
目次
・前回のあらすじ
・離散系シミュレーション…?
・目的の重要性
・離散系と連続系
・やっぱり目的の重要性
・追い込み過ぎはよくないよ
・追い込まなさすぎもよくないよ
・Emulate3Dだと何ができる??
前回のあらすじ
前回は”離散系シミュレーション”という言葉の意味を説明しました。
そして文字にしてもさっぱり伝わってこないという事が判明しました。
ざっくり言うとバラバラに起きる出来事(離散系)をシミュレーション (模擬実験) でき、それは実物や計算機で導き出すことが難しいという話でした。
第二回は例を交えて離散系シミュレーションについて更にご紹介していきます。
離散系シミュレーション…???
ある飲食店があったとします。流石に「外食したことなんてないわ!」という方はなかなか稀有だと思いますので、飲食店で発生するイベントはイメージがつきやすいと思います。 (下図)
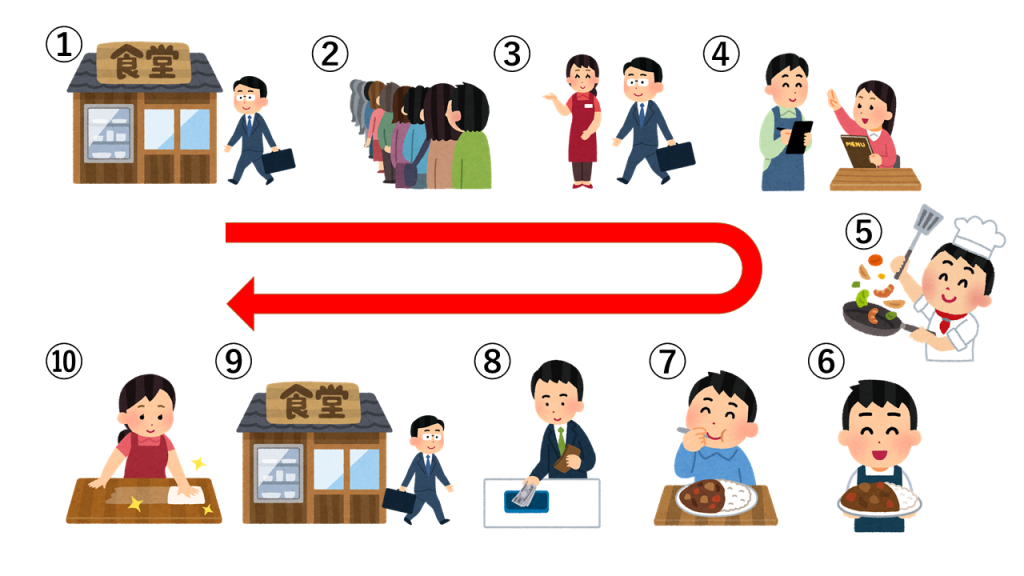
基本的な流れは①お客さんが来店する。
②(待ちがあれば)お客さんが待つ
③店員が案内する
④お客さんが注文する
⑤店員が調理する(お客さんが待つ)
⑥店員が運ぶ(お客さんが待つ)
⑦お客さんが食べる
⑧お客さんがお会計する
⑨お客さんが退店する
⑩店員が清掃する
こんな感じでしょうか。
もっと細分化も出来ますがとりあえずこんなくらいとして、
①、④、⑧のイベントの発生はランダム要素が強く、
③や⑤、⑥や⑨や⑩などはその前のイベントが終了しなければ発生しえません。
そしてこれらのイベントは①~⑩の順番で繰り返されない場合があります。
(注文を呼んでも明らかに席が空いていても掃除していたらクレームものですね)
また、離散系シミュレーションの特徴としてイベントを数えることが出来ます。
例だと「5」名のお客さんが来たとか、座席は「20」席あるとか、ランチは「10」分で調理できるとか…
こういった”モデル”に関してシミュレーションできるのが離散系シミュレーションです。
時系列上で独自の順番やランダムに実行される複数のイベントを考慮した際の最適解を得たいというのは上述の様なイベントの複雑な因果関係により計算機で求めることが難しく、意外と身近に存在している課題です。
他にもよくある例として銀行の窓口なんかがあります。(同じくお客さんはランダムに来て目的も口座開設、ATM利用など様々)
目的の重要性
さて、「離散系シミュレーションとは何か?」という結論は出ましたがシミュレーションの意味をもう一度反芻してみて下さい。
シミュレーションは対象物の理解を深めることが出来るのです。
理解を深めたい部分、解決したい課題を決めなければシミュレーションする意味がありません。
つまりシミュレーションには目的が重要となります。
今回の例であれば「ピークタイムの最適な店員の人数を知りたい」とかでしょうか。
座席数やメニューは固定値として、調理や清掃の時間をある程度の平均値を設定して店員の人数と来客数をパラメトリックに変更すれば机上でピークタイムの最適な店員の人数を導き出すことが出来ます。
※例では既に存在する飲食店に対しての目的であり、現実的に対応できる項目は店員数ですので最適な人数としましたが、
環境を新設する際に、求める能力値を満たす(例ではピークを捌ききれる)構成を検討する場合、変更できる項目は増大します。(座席数やメニュー数など)
その場合はボトルネックの顕在化という役割を離散系シミュレーションが担うことになります。
離散系と連続系
ついで程度ですが離散系ではない”連続系シミュレーション”なるものも存在します。
今回は関係ないので詳しくは書きませんが、バラバラに発生するわけではない(離散的でない)時系列での連続的な変化をシミュレーションすることです。
流体、熱伝導、電磁気学、構造解析などに用いられるようです。 前回シミュレーションの例として挙げた宇宙の膨張率や分子の安定構造はこっちになります。
離散系シミュレーションとは規模が異なりますね。
そのため離散系シミュレーションを行う際に連続系シミュレーションにより解を求め得る要素がイベントとして因果関係をもつことも多々あります。
先程の飲食店の例であれば調理する際の調理器具の材質と熱源に因る熱伝導率の関係から提供スピードのシミュレーションを行いそれを⑤の処理(店員が調理する(お客さんが待つ))の値にするとかですかね。
コンピュータで行うシミュレーションとして離散系と連続系に大別する考え方はありこそすれ、対義語という訳ではないのでご注意ください。
やっぱり目的の重要性
当たり前ですが離散系シミュレーションを実行する場合再現するレベル(”モデル”の再現度)が非常に重要となります。
前項の熱伝導まで加味した料理店のシミュレーションをするとなるとそれはそれは凄まじい性能のコンピュータとソフトウェアが必要になります。
例①~⑩のフローを細分化すればするほど設定には手間がかかってきます。
つまりシミュレーションを使って知りたいこと(目的)を明確化しないと離散系シミュレーションの効果は最大限に発揮できません。
追い込み過ぎはよくないよ
他方、目的がはっきりしていれば追い求めるべきでない項目もあるわけです。
今回の目的であれば店員の人数が知りたいだけであって調理時間の詳細な因果関係の設定や、店員の動作の再現は不要です。
作業にかかる時間の平均値をパラメトリックな値として設定してその値分の人の”モデル”がその場で待機するとかで良い筈ですね。
こういった考え方はトポロジー最適化とかKISSの原則とかで主張されています。
この部分に注意しておかないと知りたいこと(目的)がブレたり、”モデル”作成の時間が増大していきます。
逆に念頭に置いていればその課題に関する解決方法として似た課題に対しノウハウを横展開することも可能になってきます。

追い込まなさすぎもよくないよ
ここまでを踏まえもしかすると「じゃあ、最終的な最適解だけ出せばいいのでは?」と思われることがあるかもしれません。
ですが多くはそうとも言い切れません。
離散系シミュレーションは時系列での変化をシミュレーションするという点とシミュレーションの結果を確認するという部分で目的のイベントを視覚的に再現していないと認識齟齬や発見の阻害要因となります。
「これが最適解です間違いなしです!」といっても”モデル”内を俯瞰することでの気づきや他者への意思疎通のスムーズ化がきっとあるはずです。
故に”モデル”の再現度という部分は離散系シミュレーションを行う上で最も大きな課題となるのです。
つまるところ、
シミュレーションの”モデル”は対象物の理解を深めたい部分(≒目的)の特性を再現したもの
という事になります。

以上までが離散系シミュレーションに関するご説明でした。
”離散系シミュレーション”と仰々しい表現をされると難しいイメージですが、
途中でも少し触れたように、離散系シミュレーションが解を出し得る課題ってかなり汎用的な話なんですよね、、、
できることなら皆さん解決したいんじゃないかな~~~~~~~
かな~~~~~~~
な~~~~~~
~~~……
…
… はい、ではここから弊社取り扱い製品のご紹介です。
是非ここまで読んだのであればあと少しなので弊社のソリューションもご覧下さい!!
Emulate3Dだと何が出来る??
弊社取り扱い製品「Emulate3D」では離散系シミュレーションを実施できます。
(連続系も物理エンジンを搭載しているのである程度は検証できます。流体解析とかは難しいですが…)
例では飲食店でしたが、実際の製造業や物流業の課題に向けては
搬送車の最適台数(交差点制御の加味したうえでの固定値の流入量を捌ききる台数・配置)
や
ラインの成立性検証(工程間搬送や器具交換、人の作業時間による待ち、チョコ停によるランダム性の加味)
などの解決に役に立ちます。
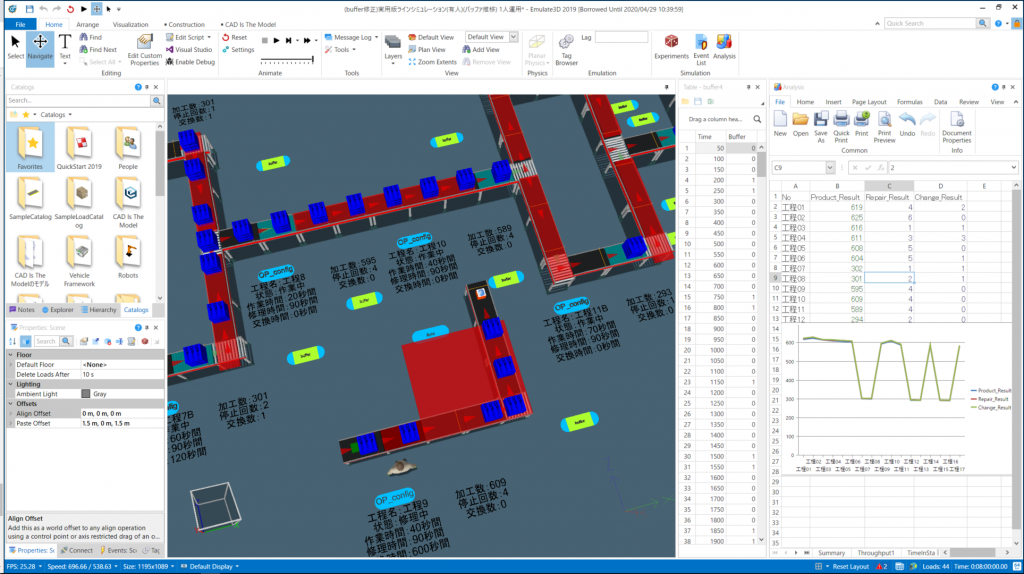
実際のユーザー様でもこういった課題に対してEmulate3Dを利用いただいている事例も多々あります。
基本的にまずEmulate3D内に”モデル”を作成するのですがデモンストレーションツールとして使うことも出来るツールですのでトポロジー最適化を図った”モデル”でもビジュアルは抜群です!!
きっとここまでお伝えした離散系シミュレーションの最適な利用をご提供できます。
離散系シミュレーションを使って解決したい課題(目的)がある方は是非、
お問い合わせいただけたらと思います。
勿論、「こんな目的があるけどEmulate3Dで解決できそう?」
というご質問もお待ちしております。
弊社が提供できる最適なソリューションをご提案させていただきます。
そんなEmulate3Dに関してもっと知りたいという方は以下の製品ページも是非合わせてご覧ください。
…因みにコンピュータだって所詮スーパー計算機ですから、当然この離散系シミュレーションが得意とする課題に関する数式化もできます。ご興味があれば『待ち行列理論』とかを調べてみると面白いかもしれません。(『待ち行列理論』=離散系シミュレーションではないのでご注意ください。)